Mathe
Auf dieser Unterseite gibt es fast nur ein Thema aus der Mathematik: den Goldenen Schnitt. Denn das ist hier mein ganz geliebtes Topic. Ein
anderes Thema ist das Teilen durch Null. - Übrigens: Ich behaupte gerne, dass Gott die Mathematik gemacht und geschaffen hat. Beweisen kann ich das allerdings
nicht.
Goldener Schnitt
Goldener Schnitt, aus wikiwand zitiert
Aus wikiwand: Ursache
ist das Bestreben dieser Pflanzen, ihre Blätter auf Abstand zu halten. Es wird vermutet, dass sie dazu an jedem Blattansatz einen besonderen Wachstumshemmer (Inhibitor) erzeugen, der im Pflanzenstamm – vor allem nach oben, in geringerem Umfang in seitlicher Richtung –
diffundiert. Dabei bilden sich in verschiedene Richtungen bestimmte Konzentrationsgefälle aus. Das nächste Blatt entwickelt sich an einer Stelle des Umfangs, wo die
Konzentration minimal ist. Dabei stellt sich ein bestimmter Winkel zum Vorgänger ein. Würde dieser Winkel den Vollkreis im Verhältnis einer rationalen Zahl 
Der Nutzen für die Pflanze könnte darin bestehen, dass auf diese Weise von oben einfallendes Sonnenlicht (bzw. Wasser und Luft) optimal genutzt wird, eine Vermutung, die bereits Leonardo da Vinci äußerte, oder im effizienteren Transport der durch Photosynthese entstandenen Kohlenhydrate im Phloemteil der Leitbündel nach unten. Die Wurzeln von Pflanzen weisen den Goldenen Winkel weniger deutlich auf. Bei anderen Pflanzen wiederum treten Blattspiralen mit anderen Stellungswinkeln zutage. So wird bei manchen Kakteenarten ein Winkel von 99,5° beobachtet, der mit der Variante der Fibonacci-Folge 1, 3, 4, 7, 11, … korrespondiert. In Computersimulationen des Pflanzenwachstums lassen sich diese verschiedenen Verhaltensweisen durch geeignete Wahl der Diffusionskoeffizienten des Inhibitors provozieren.
Bei vielen nach dem Goldenen Schnitt organisierten Pflanzen bilden sich in diesem Zusammenhang so genannte Fibonacci-Spiralen aus. Spiralen dieser Art sind besonders gut zu erkennen, wenn der Blattabstand im Vergleich zum Umfang der Pflanzenachse besonders klein ist ... (Zitat-Ende; aus Wikiwand)
Ich hätte das obige "Stück" aus wikiwand gern gekürzt, habe ich dann aber doch so lang gelassen. Man sagt vielleicht besser: Ursache des Goldenen Schnittes ist Gott selbst. Denn Er, der Schöpfer-Gott, hat diesen idealen Schnitt ja verursacht und geschaffen. Gott erschafft souverän nach mathematischen Gesetzen!
"Fibonacci"
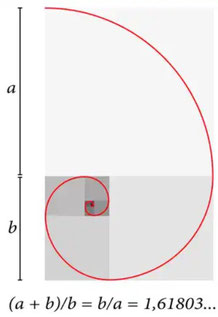
Hängen zusammen: Der Goldene Schnitt und die Fibonacci-Zahlen.
Der Goldene Schnitt (ca. 1,618 : 1) kommt fast überall in der Natur vor; sogar in den Körpermaßen des Menschen ist er zu finden. Auch zeigt er sich in dem idealen Winkel von 137,5 ° (degree, deg). Dieser Winkel kommt in der Natur beim Blattabstand vor.
Die Fibonacci- oder Goldene-Schnitt-Formel: a / b = ( a + b ) / a
bzw.
a / b = φ = 1.618033988749895
Das genau trifft zu für sehr hohe Fibonacci-Zahlen.
Wie erhalte ich den Goldenen Schnitt?
Wenn ich eine Linie (A) folgendermaßen teile:
Das Verhältnis der Gesamtstrecke A zu der Teilstrecke B muss dasselbe sein wie das Verhältnis von B zu C.
Der Goldene Schnitt kommt überall in der Natur vor. Menschen finden Dinge schön, die der Natur ähneln. Wir sind geradezu versessen auf Symmetrie.
Es ist für den normalen Schüler ein Geheimnis: Der Goldene Schnitt kommt überall in der von Gott erschaffenen Natur vor, bei Pflanzen, bei Tieren und auch beim Menschen. Überall in fast allen Schneckenhäusern und im Schwanz des Seepferdchens zum Beispiel sieht man diese Goldene Regel, diese für unsere Augen schöne "Verteilung". Darum sieht die Natur so harmonisch, so symmetrisch aus. Man braucht die Fibonacci-Reihe (0,1,1,2,3,5,8,13,21,34,55,89,144,233 usw.) nicht einmal weit in die Hunderttausende oder Millionen zu treiben, das Verhältnis einer Zahl in der Fibonacci-Folge zur nächstkleineren Zahl ist schnell näherungsweise der Goldene Schnitt (recht genau: 1,618033989; genauer gesagt oder geschrieben ist der Goldene Schnitt (1+sqrt(5))/2). Überall in der Natur, ja sogar in der DNA, kommt dieser Schnitt vor.
Es ist wissenschaftlich erwiesen, dass die Goldene Regel ganz oft in der Natur, also in der Schöpfung unseres allmächtigen Gottes, vorkommt. Es geht schon los beim Menschen. Da braucht man nur folgende Strecken zu messen, und es ergibt sich sehr genau der Goldene Schnitt. Auch das Verhältnis von Körpergröße und Bauchnabelhöhe ist so leicht messbar. Man braucht nur vom Kopf bis zur Fußsohle und danach vom Bauchnabel bis zur Fußsohle messen. Es ergibt sich ein erstaunlich exaktes Verhältnis von 1,618.
Weitere Mathethemen
Algebra
Ein Beispiel
1/5 * x^5 = 125 * x
Bei der Betrachtung der mathematischen Aufgabe 1/5 * x^5 = 125 * x ist es wichtig zu erkennen, dass 0 tatsächlich eine gültige Lösung darstellt. Dies lässt sich
folgendermaßen begründen:
Nullstelle als Lösung
Wenn wir x = 0 in die Gleichung einsetzen, erhalten wir: 15⋅05=125⋅051⋅05=125⋅0 Beide Seiten der Gleichung ergeben 0, was bedeutet, dass die Gleichung für x = 0 erfüllt ist.
Algebraische Umformung
Um dies weiter zu verdeutlichen, können wir die Gleichung umformen:
Multiplizieren wir beide Seiten mit 5:
x5=625xx5=625x
Bringen wir alle Terme auf eine Seite:
x5−625x=0x5−625x=0
Faktorisieren wir den Ausdruck:
x(x4−625)=0x(x4−625)=0
Mathe-Wiki oder "LuckyLogic" - das sind Webseiten, die ich noch nicht kenne ...
Linktipps
Und wer es noch ausführlicher und auch komplizierter haben muss, der gehe auf mathworld.wolfram.com!
Durch 0 teilen undefiniert
Die folgenden Videos ist englisch und behandeln das Thema, ob Teilen durch null vielleicht unendlich (mathematisches Zeichen: ∞) oder nicht definiert ist.
Ich vermute, dass folgende Begründung hinreichend ist: Die zwei Ergebnisse von x durch 0 sind ja quasi "plus Unendlich" und "minus Unendlich". Darum ist es sehr schwer zu begreifen; also ist das Durch-Null-Teilen "nicht definiert".